


Next: Elastic-Plastic Constitutive Law
Up: CALIBRATION OF ELASTIC-PLASTIC MATERIAL
Previous: Introduction
Elastic Cross-Anisotropic Constitutive Law
The linear, small-strain, elastic behavior of cross-anisotropic material
is governed by the following generalized Hooke's law [4]:
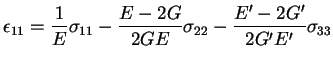 |
(1) |
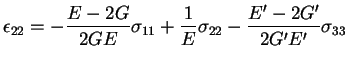 |
(2) |
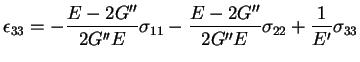 |
(3) |
where, in equation (1)
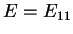 = in-plane Young's modulus;
= in-plane Young's modulus;
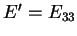 =
out-of-plane Young's modulus;
=
out-of-plane Young's modulus;
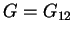 = in-plane shear modulus;
= in-plane shear modulus;
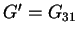 = out-of-plane shear modulus;
= out-of-plane shear modulus;
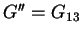 = out-of-plane
shear modulus. Note that ''in-plane'' refers to the 1-2 isotropy plane
(horizontal) and ''out-of-plane'' refers to the 3-direction (assumed vertical).
= out-of-plane
shear modulus. Note that ''in-plane'' refers to the 1-2 isotropy plane
(horizontal) and ''out-of-plane'' refers to the 3-direction (assumed vertical).
The above elastic material constants, 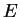 ,
, 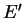 ,
, 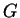 ,
, 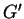 , and
, and 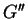 can be
determined from three-dimensional P-wave and shear wave tests. The equation
relating in-plane Young's modulus (
can be
determined from three-dimensional P-wave and shear wave tests. The equation
relating in-plane Young's modulus (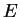 ) and in-plane P-wave velocity
(
) and in-plane P-wave velocity
(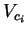 ;
; 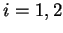 ) is,
) is,
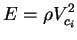 |
(5) |
Similarly, the equation relating out-of-plane Young's modulus (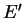 ) and
out-of-plane P-wave velocity (
) and
out-of-plane P-wave velocity (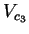 ) is,
) is,
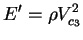 |
(6) |
The equation relating in-plane shear modulus (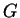 ) and in-plane shear wave velocity with horizontal polarization (
) and in-plane shear wave velocity with horizontal polarization (
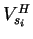 ;
; 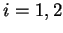 ) is,
) is,
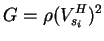 |
(7) |
where wave propagation is in the i-direction (i=1,2) with horizontal
polarization. The equation relating out-of-plane shear modulus (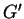 )
and out-of-plane shear wave velocity (
)
and out-of-plane shear wave velocity (
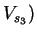 is,
is,
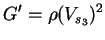 |
(8) |
where wave propagation is in the 3-direction with
horizontal polarization.
Finally, the equation relating out-of-plane shear modulus (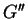 ) and
in-plane
shear wave velocity with vertical polarization (
) and
in-plane
shear wave velocity with vertical polarization (
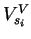 ;
; 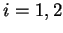 )
is,
)
is,
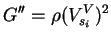 |
(9) |
where wave propagation is in the i-direction (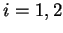 )
with vertical polarization.
)
with vertical polarization.



Next: Elastic-Plastic Constitutive Law
Up: CALIBRATION OF ELASTIC-PLASTIC MATERIAL
Previous: Introduction
Boris Jeremic
2003-11-14
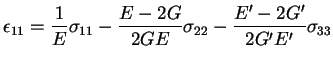
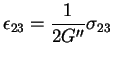 ;
;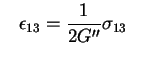 ;
;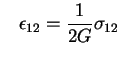
![]() ,
, ![]() ,
, ![]() ,
, ![]() , and
, and ![]() can be
determined from three-dimensional P-wave and shear wave tests. The equation
relating in-plane Young's modulus (
can be
determined from three-dimensional P-wave and shear wave tests. The equation
relating in-plane Young's modulus (![]() ) and in-plane P-wave velocity
(
) and in-plane P-wave velocity
(![]() ;
; ![]() ) is,
) is,